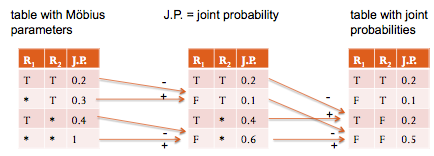
Class-level dependencies model general relational statistics over attributes of linked objects and links. Class-level relationships are important in themselves, and they support applications like policy making, strategic planning, and query optimization. An example of a classlevel query is “what is the percentage of friendship pairs where both friends are women?”. To represent class-level statistics, we utilize Parametrized Bayes nets (PBNs), a 1st-order logic extension of Bayes nets. The standard grounding semantics for PBNs is appropriate for answering queries about specific ground facts but not appropriate for answering queries about classes of individuals. We propose a random selection semantics for PBNs, based on Halpern’s classic semantics for probabilistic 1storder logic [1], that supports class-level queries. Learning the parameters for this semantics can be done using the recent relational BN pseudolikelihood measure [2] as the objective function. The parameter settings that maximize this objective function are the empirical frequencies in the relational data. A naive computation of the empirical frequencies of the relations is intractable due to the complexity imposed by negated relations. We render the computation tractable by using the fast Möbius transform. Evaluation on four benchmark datasets shows that maximum pseudo-likelihood provides accurate estimates at different sample sizes.